06 - Multi-Layer Perceptron-Networks

"Now we are talking about something that is not linear"

XOR: A Limitation of the Linear Model

• Linear model: just 2 layers: input layer and output layer
• One way to make this model not linear is to make it wider (still 2 layers)
• This is called kernel methods
  • How to make it wider? you make the input vector to be larger?
  • Usually we do not count the softmax layer
  • The way to make it wider is to apply $\varphi (x)$
    • Now $x$ is a wider vector
    • This model will be not linear in terms of $x$
  • How do we do transformations to a vector $x$?
    • We apply $\varphi$ transformations
    • $\varphi$ is a vector that makes the $x$ components be multiplied by some other $x$ components.
    • You end up increasing the dimension of $x$
• In training, you only need this: $$\phi^T(x_i)\phi(x_j) = (x_i^Tx_j)$$
  • The pairwise inner product with $\varphi$
• There is a more efficient way to do this, which is deep learning (making a model to be deep)
• Kernel methods = use pairwise inner product
  • Can be computed very efficient

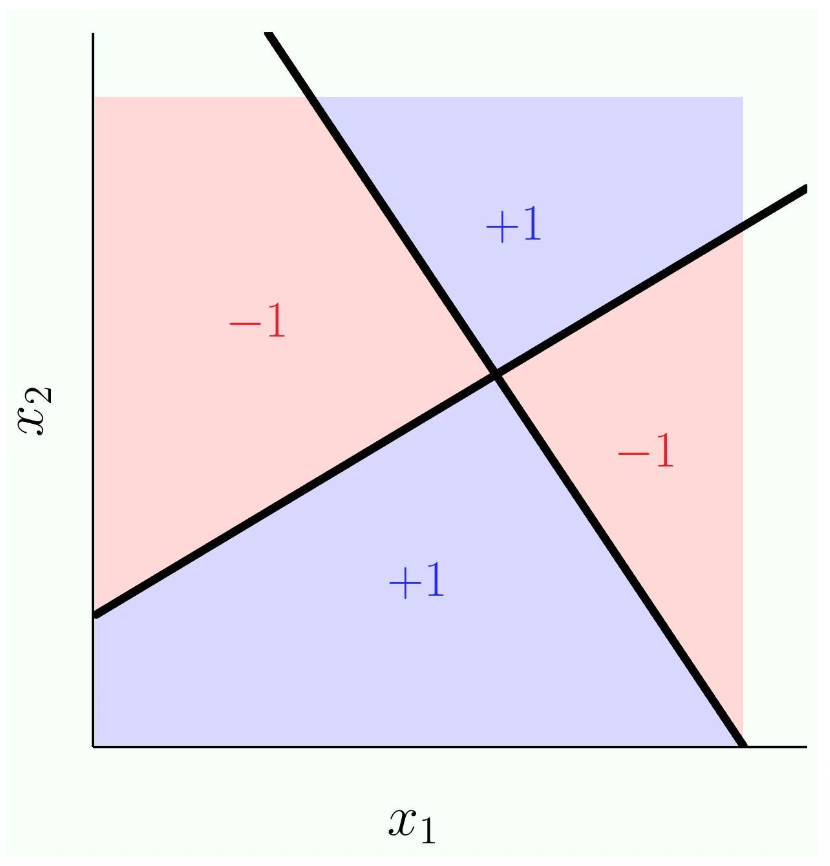
Decomposing XOR

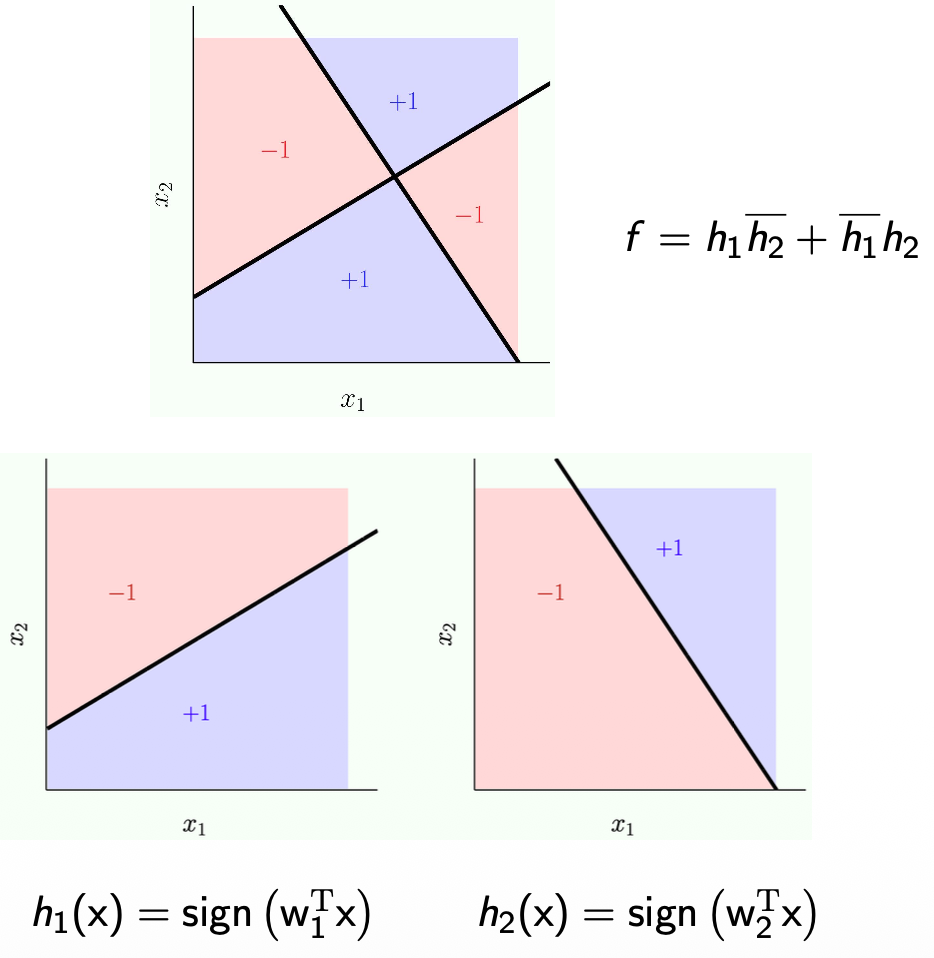
• Exclusive OR: $f=h_1\overline{h_2}+\overline{h_1}{h}_2$
• Basically means:
  • If $h_1$ and $h_2$ both give you positive or negative, the result is negative (-1).
  • They need to be different for XOR to output positive (+1)
• So they key here is that we use linear models but we use multiple of them and we put them together

Perceptrons for OR and AND

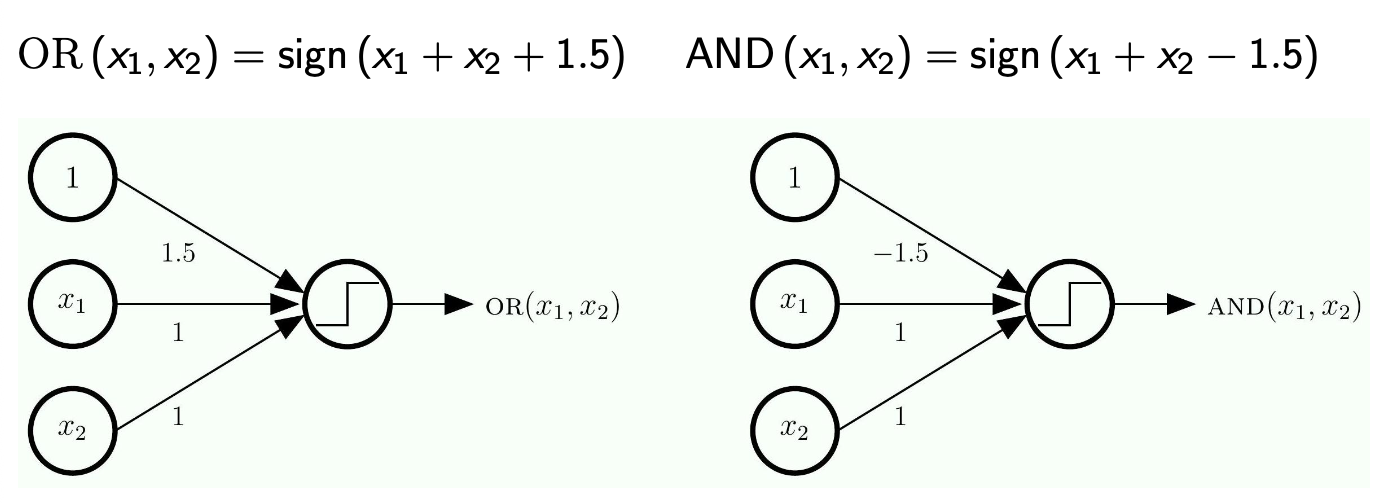
• OR:
  • If one or both of $x_1$ and $x_2$ is positive, then OR is positive
  • Why +1.5?
    • It is just needed to represent OR
    • It will just represent the truth table.
    • The input for $x_1$ and $x_2$ is just +1 or -1
• AND:
  • If both $x_1$ and $x_2$ are positive, then AND is positive

Representing $f$ Using OR and AND

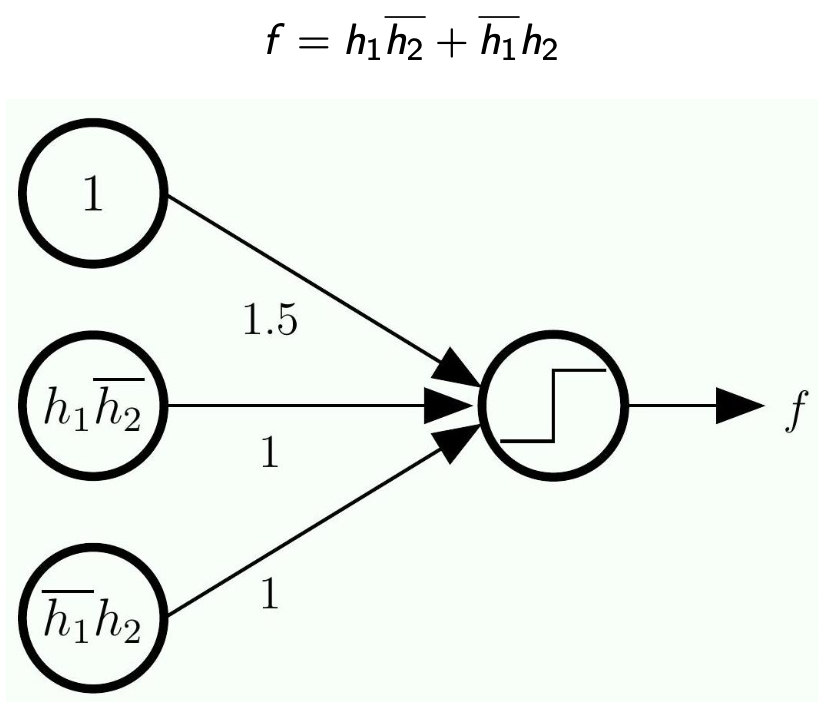
• Here we work backward because we are given $f=h_1\overline{h_2}+\overline{h_1}{h}_2$
• We need to expand each of $h_1{h}_2$
• Here, $h_1{h}_2$ is the input and the output is $f$

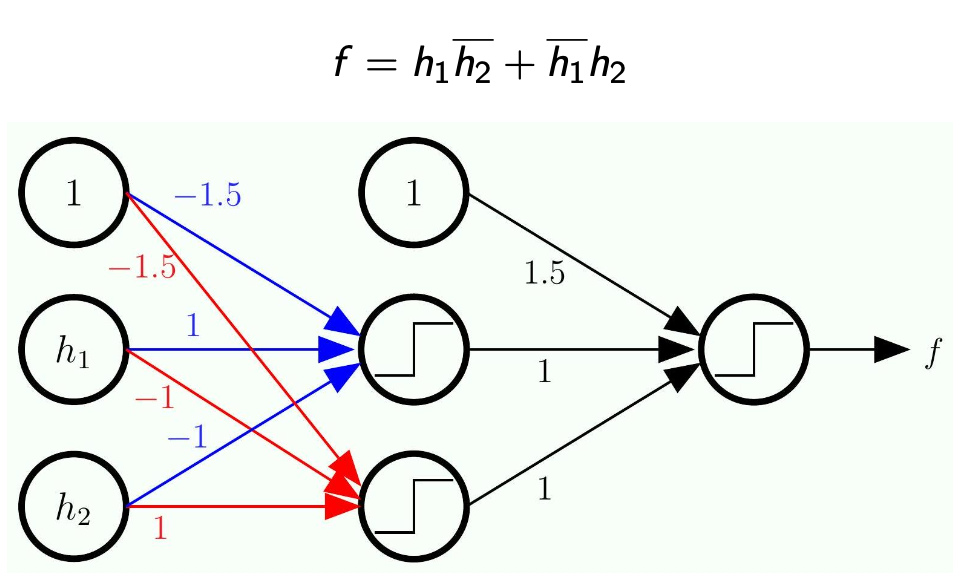
• The next step is to expand each of $h$
  • Note that each of $h_i$ is a linear model of the input
• The -1.5 will eliminate the term we added to implement OR/AND
• Note the bar on the top means $-1$

• Now, since we know each of $h_i$ is a linear model of the inputs $x_1$ and $x_2$, then we decompose even more

• Note how this became a network with multiple layers!

• Nothing is trained here

  • This is just a completely hardwire network
  • Solves problems that linear models cannot solve by their own

• Will this method enable us to do more complex models? (something more complex than $f=h_1\overline{h_2}+\overline{h_1}{h}_2$)

  • Yes! you can always convert any logic function into this form
  • As long as you can convert to this standard form you will be used to use a network just like this
    • The logic form will just look longer

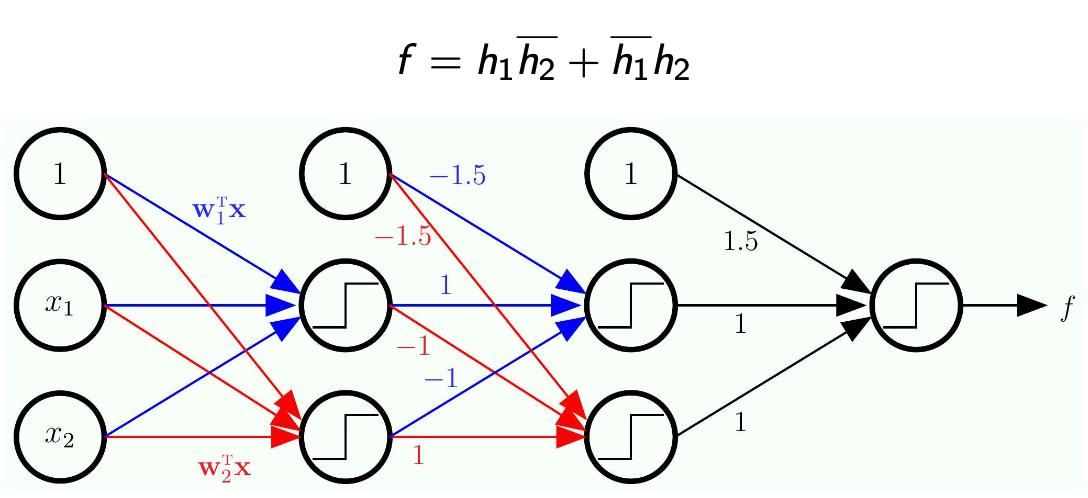
The Multilayer Perceptron (MLP)

• More layers allow us to implement $f$
• These additional layers are called hidden layers

Universal Approximation

• Any target function $f$ that can be decomposed into linear separators can be implemented by a 3 -layer MLP.
• A sufficiently smooth separator can "essentially" be decomposed into linear separators.

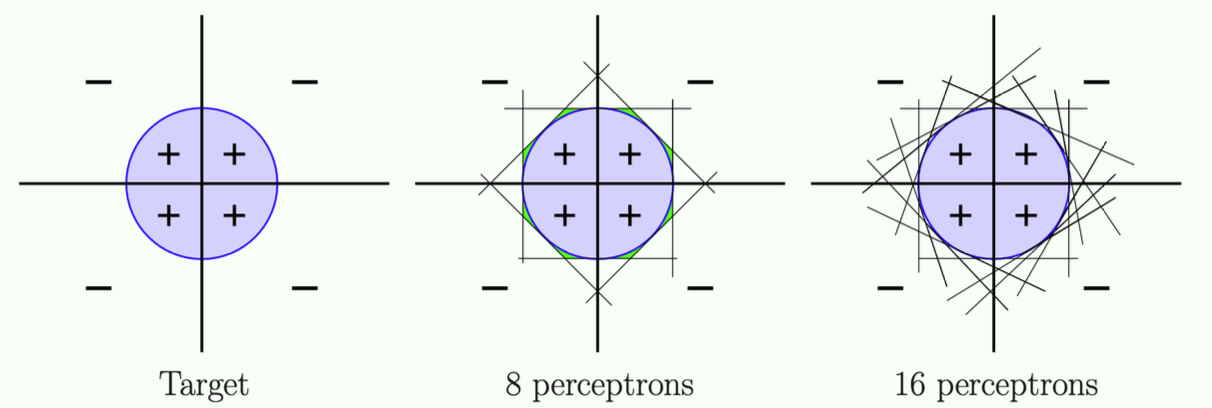
Theory:

• More units/More linear models -> more accurate predictions

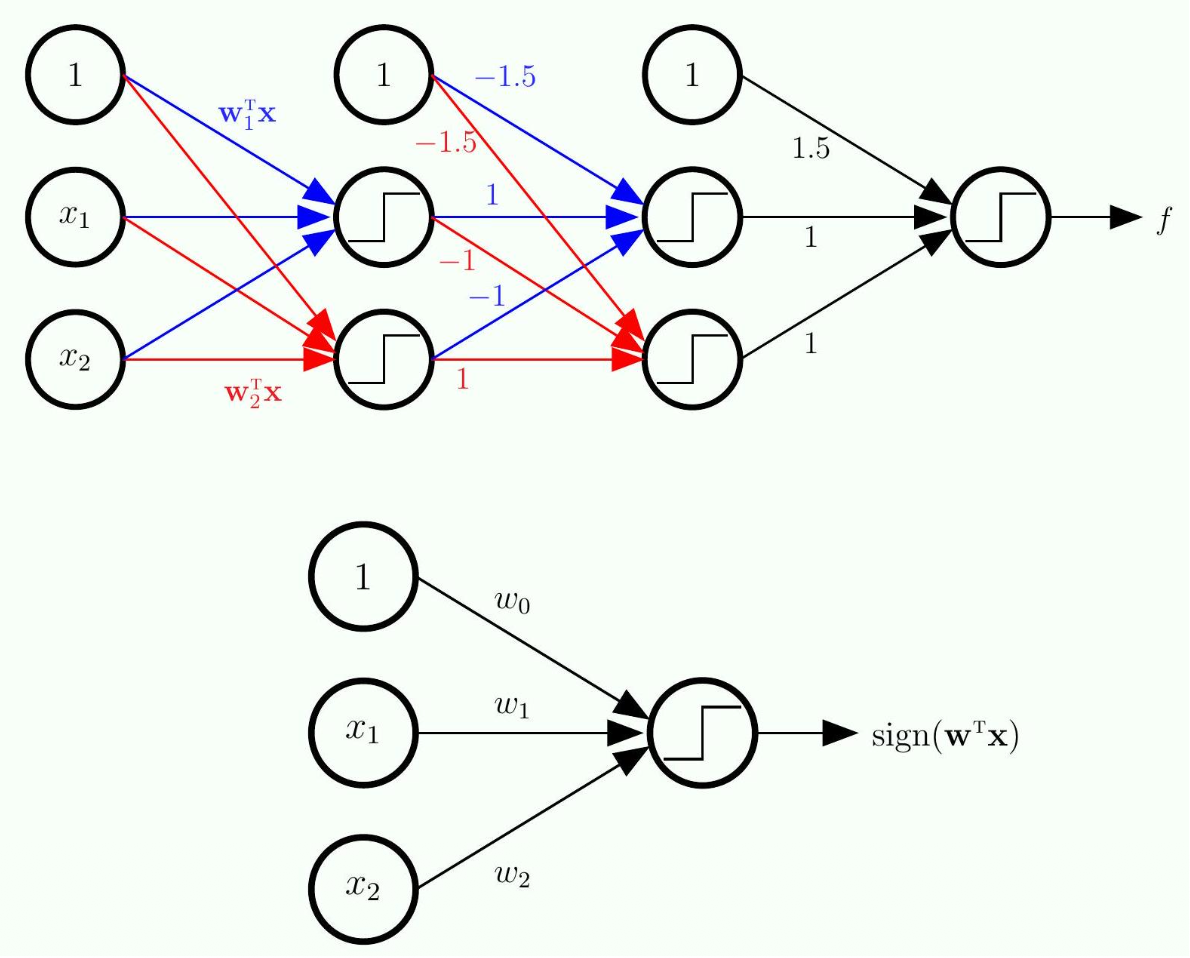
The Neural Network

• $E_{\text{in }}$ is not smooth (due to sign function), so cannot use gradient descent.
• $\mathrm{sign}(x)\approx \tan (x)⟶$ gradient descent to minimize $E_{\mathrm{in}}$.

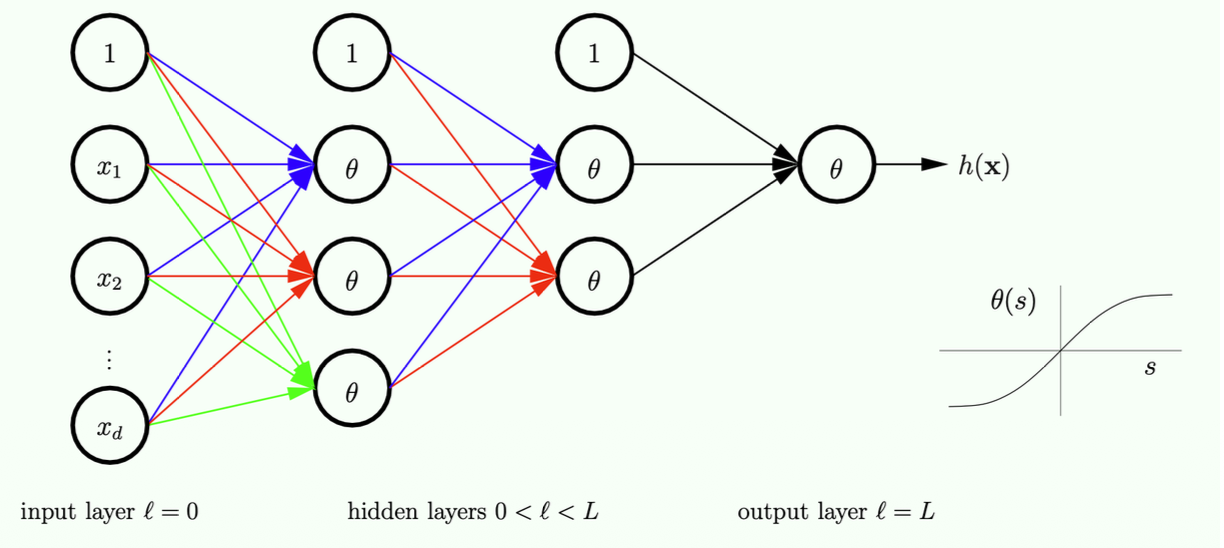
• $\theta$ needs to be differentiable
• This function has been used for many years, until recently we changed this, but we will talk about this later
• Note: we use training data to determine all the weights here.
• The question is how do we obtain those connection weights?
  • If I have this values on the left, how do we compute the values on the right (on the next layer)
• The "1" on each layer is essentially the threshold term
  • That is why this unit will have no input, but will have an output of a fixed value

Zooming into a Hidden Node

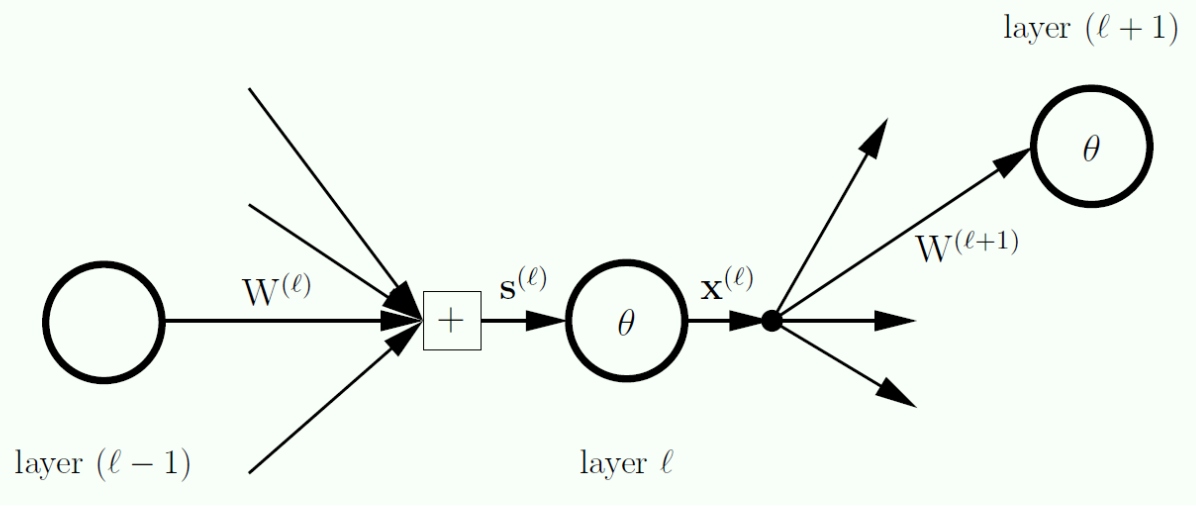
layer $\ell$ parameters (notations)

layers $\ell =0,1,2,\dots ,L$
layer $\ell$ has "dimension" ${\mathit{d}}^{(\ell )}⟹{\mathit{d}}^{(\ell )}+1$ nodes

Notes:

• What are the operations to move between layers?
• For each layer we have a signal ($s$) go into a particular layer
• For each layer we want to put the inputs for each unit into a vector, this vector is called ${\mathbf{s}}^{(\ell )}$
  • Note that ${\mathit{d}}^{(\ell )}$ does not consider the bias term
• Summary: each layer has an input vector, and an output vector
• At the end we will build a matrix where each row is one column (one layer)
• What would be the size of this matrix?
  • ${\mathit{d}}^{(\ell -1)}+1\times {\mathit{d}}^{(\ell )}$
    • This will be on the exam!

The Linear Signal

Input ${\mathbf{s}}^{(\ell )}$ is a linear combination (using weights) of the outputs of the previous layer ${\mathrm{x}}^{(\ell -1)}$.

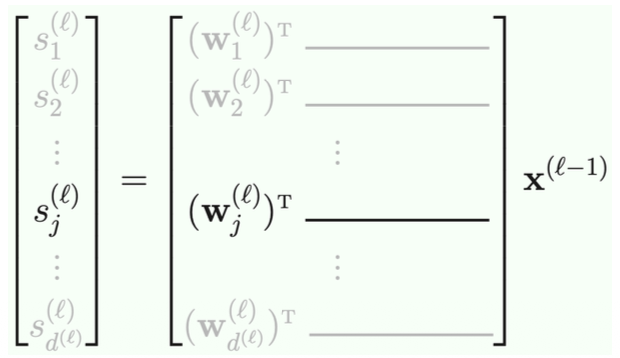
The question:

• If I have the input for one layer, how do we calculate the output?
  • What is the operation? This is $\theta$
    • We need to take a vector and apply $\theta$ to every element (element-wise product with $\theta$)
• Now, If I know the output values for this layer, how do we calculate the input values for the next layer?
  • If you look at the graph, the input of every unit depends on the outputs of the previous layers, but how do we do this?
  • What else do we need? -> the weights
    • We need to take 1 column from the weights matrix.
    • Remember the rows of the weights matrix is composed of the previous layer number of of units as rows and the next layer number of units as columns
      • For example between the second (1, $\theta$, $\theta$, $\theta$) and third layers (1, $\theta$, $\theta$) in the example above we will have a 4 * 2 matrix
      • In order to multiply the weights times the $x$ vector you need to do $x{W}^T$ to account for the different number of rows and columns on each vector/matrix