06 - Multi-Layer Perceptron-Networks

"Now we are talking about something that is not linear"

XOR: A Limitation of the Linear Model

• Linear model: just 2 layers: input layer and output layer
• One way to make this model not linear is to make it wider (still 2 layers)
• This is called kernel methods
  • How to make it wider? you make the input vector to be larger?
  • Usually we do not count the softmax layer
  • The way to make it wider is to apply $\varphi (x)$
    • Now $x$ is a wider vector
    • This model will be not linear in terms of $x$
  • How do we do transformations to a vector $x$?
    • We apply $\varphi$ transformations
    • $\varphi$ is a vector that makes the $x$ components be multiplied by some other $x$ components.
    • You end up increasing the dimension of $x$
• In training, you only need this: $$\phi^T(x_i)\phi(x_j) = (x_i^Tx_j)$$
  • The pairwise inner product with $\varphi$
• There is a more efficient way to do this, which is deep learning (making a model to be deep)
• Kernel methods = use pairwise inner product
  • Can be computed very efficient

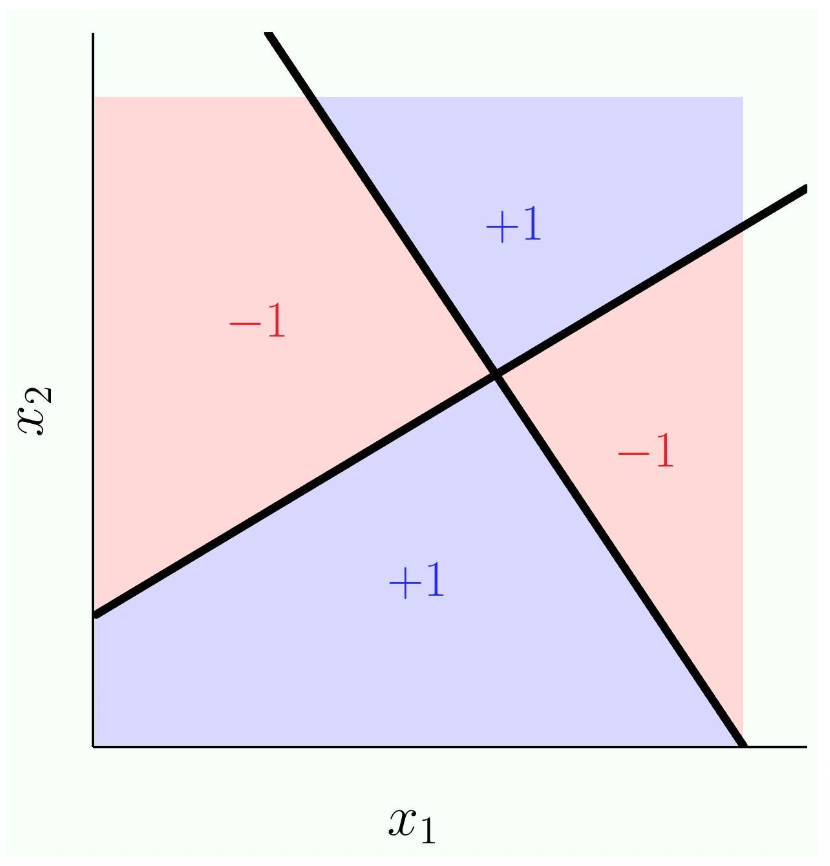
Decomposing XOR

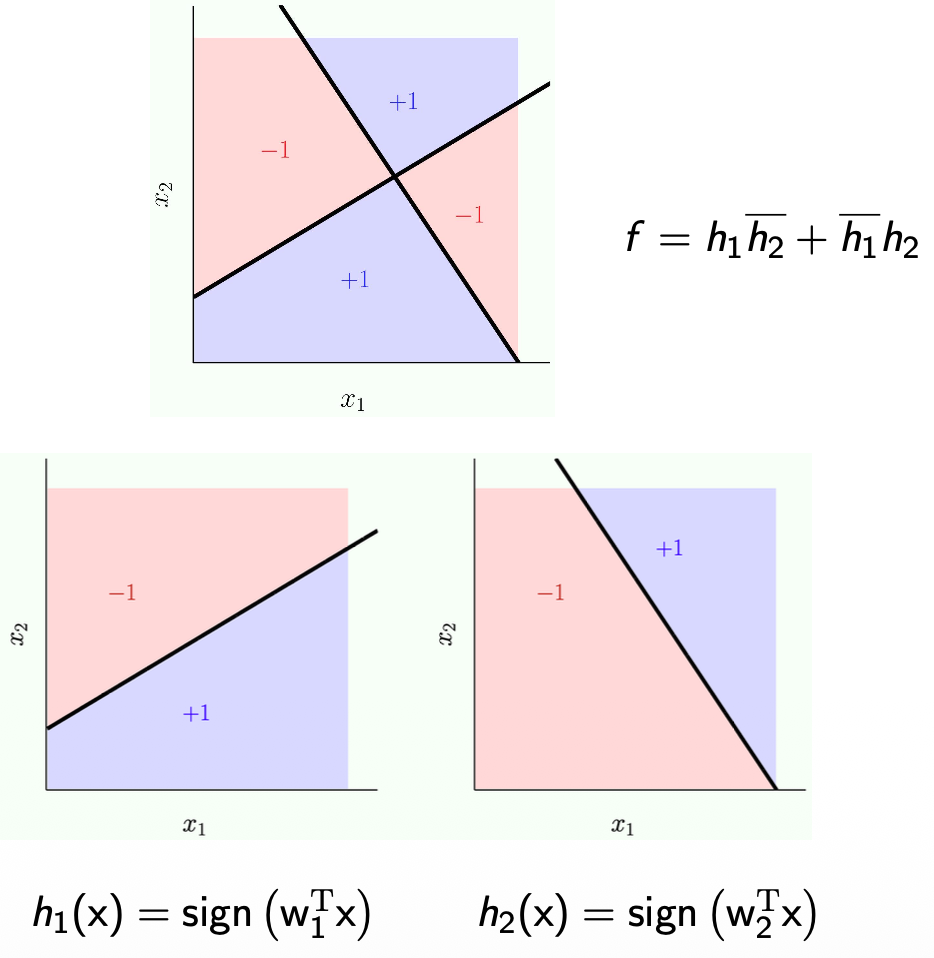
• Exclusive OR: $f=h_1\overline{h_2}+\overline{h_1}{h}_2$
• Basically means:
  • If $h_1$ and $h_2$ both give you positive or negative, the result is negative (-1).
  • They need to be different for XOR to output positive (+1)
• So they key here is that we use linear models but we use multiple of them and we put them together

Perceptrons for OR and AND

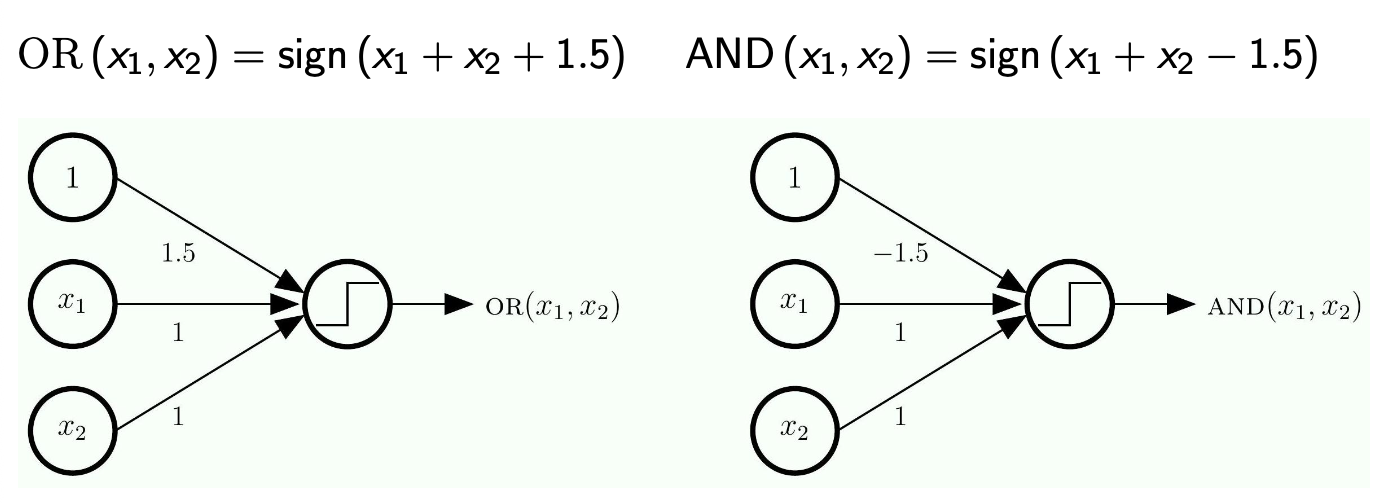
• OR:
  • If one or both of $x_1$ and $x_2$ is positive, then OR is positive
  • Why +1.5?
    • It is just needed to represent OR
    • It will just represent the truth table.
    • The input for $x_1$ and $x_2$ is just +1 or -1
• AND:
  • If both $x_1$ and $x_2$ are positive, then AND is positive

Representing $f$ Using OR and AND

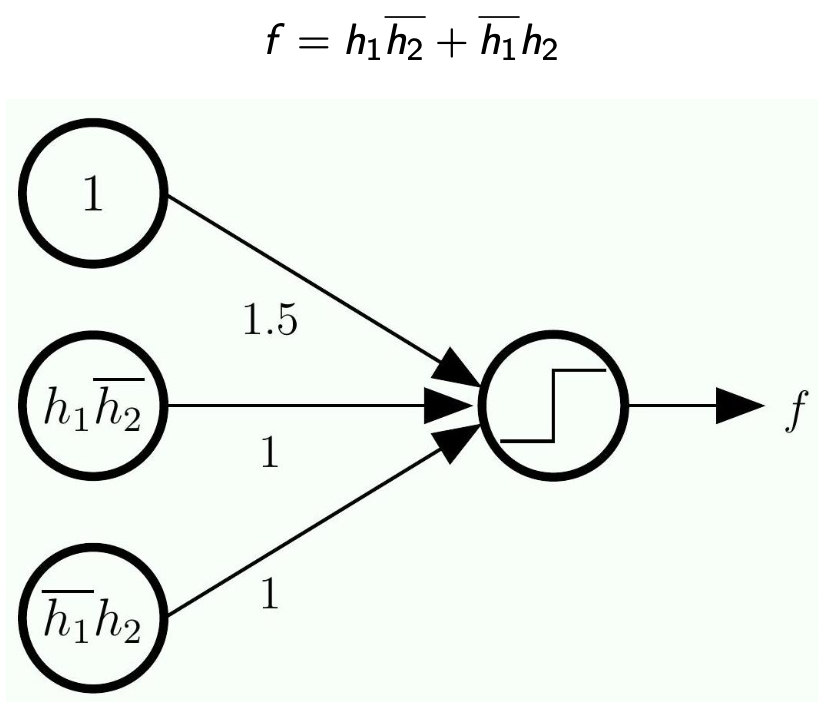
• Here we work backward because we are given $f=h_1\overline{h_2}+\overline{h_1}{h}_2$
• We need to expand each of $h_1{h}_2$
• Here, $h_1{h}_2$ is the input and the output is $f$

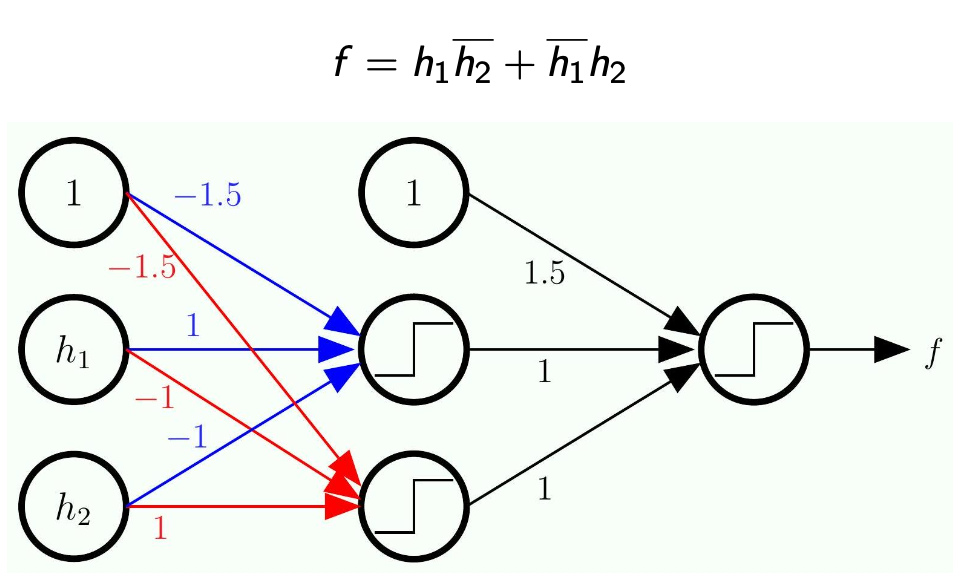
• The next step is to expand each of $h$
  • Note that each of $h_i$ is a linear model of the input
• The -1.5 will eliminate the term we added to implement OR/AND
• Note the bar on the top means $-1$

• Now, since we know each of $h_i$ is a linear model of the inputs $x_1$ and $x_2$, then we decompose even more

• Note how this became a network with multiple layers!

• Nothing is trained here

  • This is just a completely hardwire network
  • Solves problems that linear models cannot solve by their own

• Will this method enable us to do more complex models? (something more complex than $f=h_1\overline{h_2}+\overline{h_1}{h}_2$)

  • Yes! you can always convert any logic function into this form
  • As long as you can convert to this standard form you will be used to use a network just like this
    • The logic form will just look longer

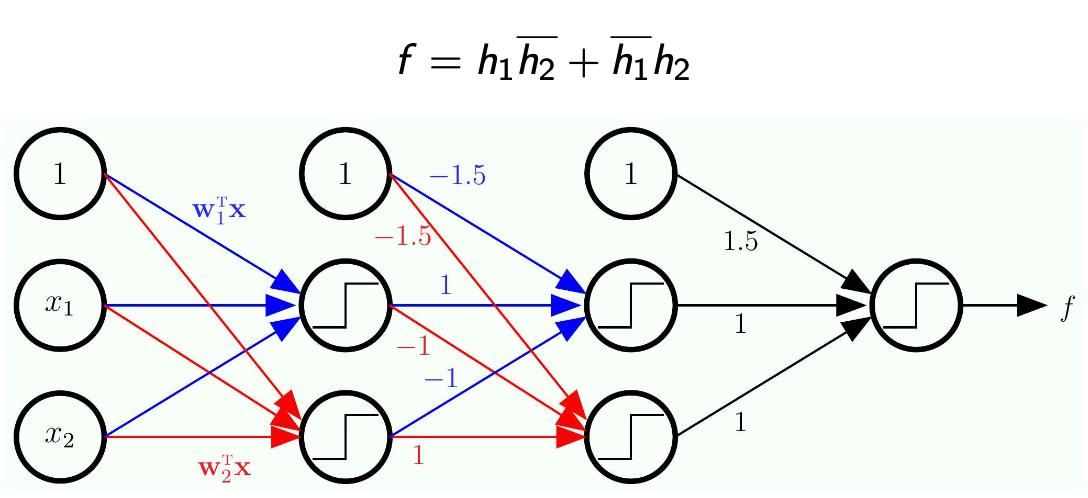
The Multilayer Perceptron (MLP)

• More layers allow us to implement $f$
• These additional layers are called hidden layers

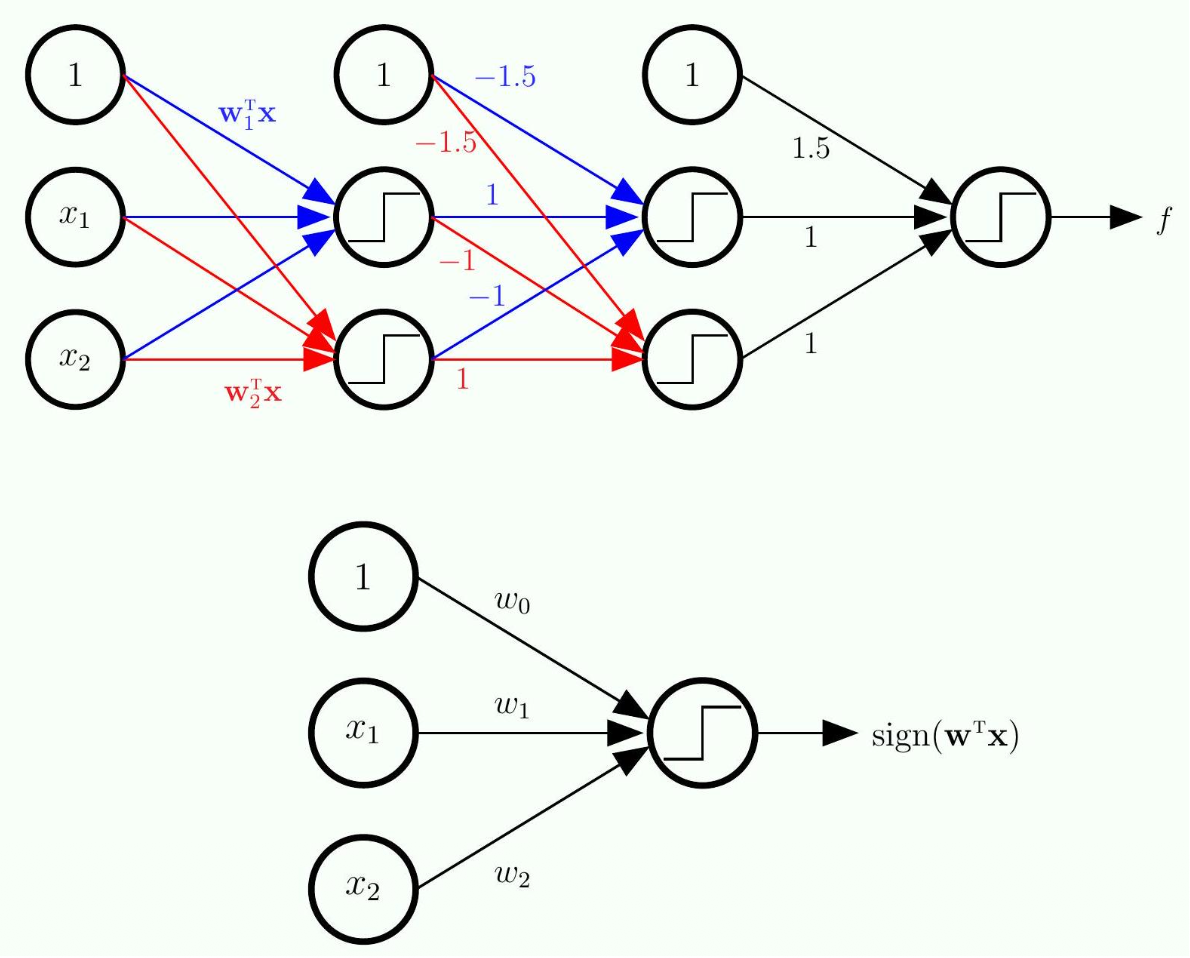
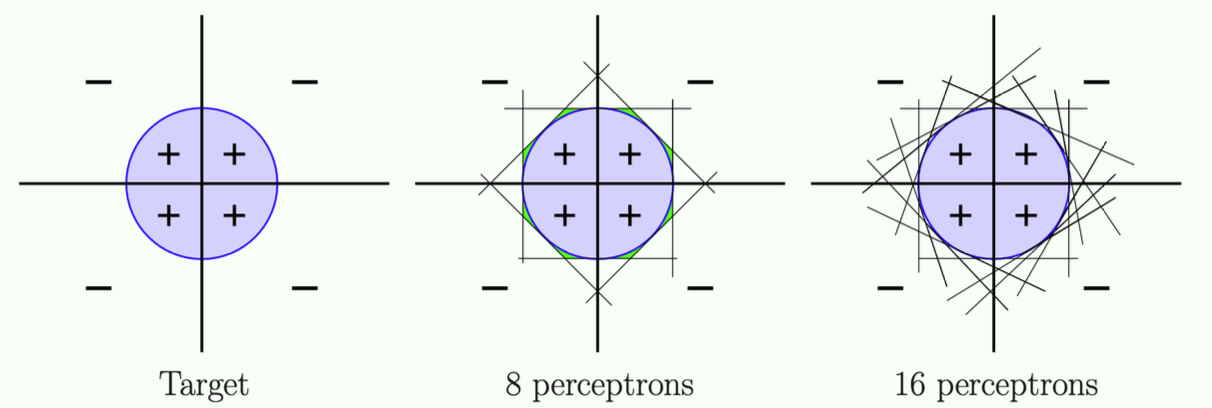
Universal Approximation

• Any target function $f$ that can be decomposed into linear separators can be implemented by a 3 -layer MLP.
• A sufficiently smooth separator can "essentially" be decomposed into linear separators.

Theory:

• More units/More linear models -> more accurate predictions

The Neural Network

• $E_{\text{in }}$ is not smooth (due to sign function), so cannot use gradient descent.
• $\mathrm{sign}(x)\approx \tan (x)⟶$ gradient descent to minimize $E_{\mathrm{in}}$.

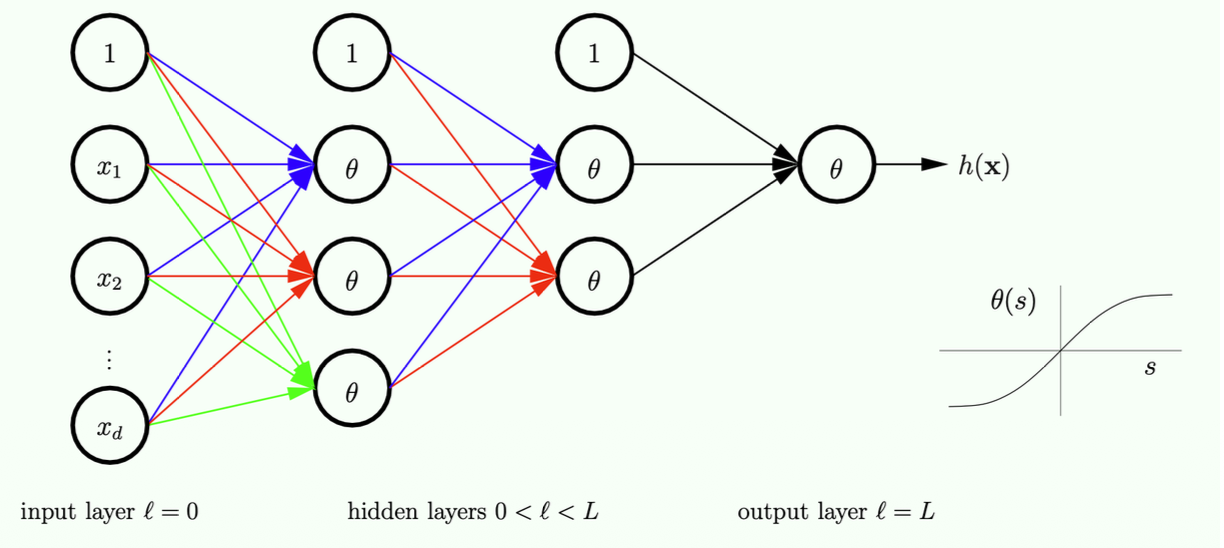
• $\theta$ needs to be differentiable
• This function has been used for many years, until recently we changed this, but we will talk about this later
• Note: we use training data to determine all the weights here.
• The question is how do we obtain those connection weights?
  • If I have this values on the left, how do we compute the values on the right (on the next layer)
• The "1" on each layer is essentially the threshold term
  • That is why this unit will have no input, but will have an output of a fixed value
• Note this is not necessarily the most economical way
  • If you use more layers, the total number of units might be smaller, that is why people usually do many many layers, even thousands

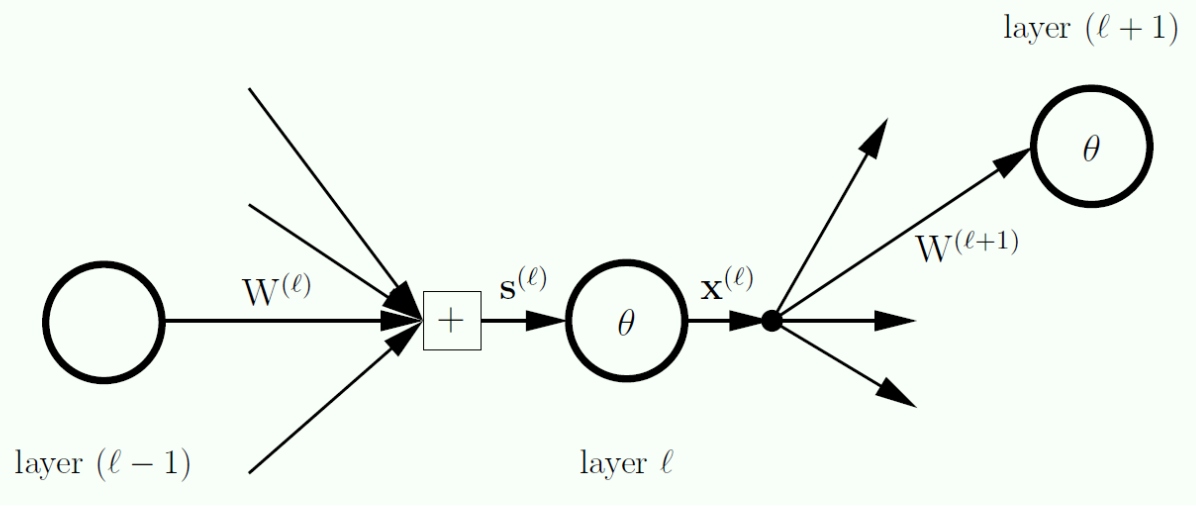
Zooming into a Hidden Node

layer $\ell$ parameters (notations)

layers $\ell =0,1,2,\dots ,L$
layer $\ell$ has "dimension" ${\mathit{d}}^{(\ell )}⟹{\mathit{d}}^{(\ell )}+1$ nodes

Notes:

• What are the operations to move between layers?
• For each layer we have a signal ($s$) go into a particular layer
• For each layer we want to put the inputs for each unit into a vector, this vector is called ${\mathbf{s}}^{(\ell )}$
  • Note that ${\mathit{d}}^{(\ell )}$ does not consider the bias term
• Summary: each layer has an input vector, and an output vector
• At the end we will build a matrix where each row is one column (one layer)
• What would be the size of this matrix?
  • ${\mathit{d}}^{(\ell -1)}+1\times {\mathit{d}}^{(\ell )}$
    • This will be on the exam!

The Linear Signal

Input ${\mathbf{s}}^{(\ell )}$ is a linear combination (using weights) of the outputs of the previous layer ${\mathrm{x}}^{(\ell -1)}$.

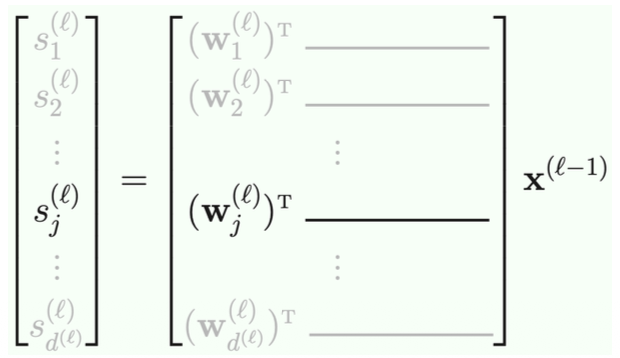
The question:

• If I have the input for one layer, how do we calculate the output?
  • What is the operation? This is $\theta$
    • We need to take a vector and apply $\theta$ to every element (element-wise product with $\theta$)
• Now, If I know the output values for this layer, how do we calculate the input values for the next layer?
  • If you look at the graph, the input of every unit depends on the outputs of the previous layers, but how do we do this?
  • What else do we need? -> the weights
    • We need to take 1 column from the weights matrix.
    • Remember the rows of the weights matrix is composed of the previous layer number of of units as rows and the next layer number of units as columns
      • For example between the second (1, $\theta$, $\theta$, $\theta$) and third layers (1, $\theta$, $\theta$) in the example above we will have a 4 * 2 matrix
      • In order to multiply the weights times the $x$ vector you need to do $x{W}^T$ to account for the different number of rows and columns on each vector/matrix
• The question here is, given the input of a layer, how do we compute the input for the next layer?
  • The operation is simple, you just apply $\theta$
  • Take that vector, apply $\theta$ element-wise and add a 1 (the threshold)
  • Of course the output, by convention needs to be a column vector
  • This is how you get to the form: $s_j^{(\ell )}={\left(w_j^{(\ell )}\right)}^{\mathrm{T}}{\mathrm{x}}^{(\ell -1)}$
• All of this will be in the exam
  • Will ask for number of parameters and stuff

Forward Propagation: Computing $h(x)$

Forward propagation to compute $h(\mathrm{x})$:

1. ${\mathrm{X}}^{(0)}\leftarrow \mathrm{X}$
   • [Initialization]
2. for $\ell =1$ to $L$ do
   • [Forward Propagation]
3. ${\mathrm{S}}^{(\ell )}\leftarrow {\left({\mathrm{W}}^{(\ell )}\right)}^{\mathrm{T}}{\mathrm{x}}^{(\ell -1)}$
4. ${\mathrm{X}}^{(\ell )}\leftarrow \left[\begin{array}{c}1\\ \theta \left({\mathrm{s}}^{(\ell )}\right)\end{array}\right]$
5. end for
6. $h(\mathrm{x})={\mathrm{x}}^{(L)}$
   • [Output]

Notes:

• You have x, where you want to make preditions
• Input layer is x(0), (there is no $\theta$ in the input layer)
• To compute the input to the next layer we apply $w(1)$, then to get to the next layer you apply $\theta$, and so on, you repeat this process.
• There are 2 operations to reach a next layer

Minimizing Ein

Using $\theta =\tanh$ makes $E_{\text{in }}$ differentiable so we can use gradient descent ⟶ local minimum.

Notes:

• Now this is about prediction.
• A backward propagation is to adjust weights after a training process and then you need to do forward propagation
• The cost of training the network using a simple example is twice the price of doing a prediction
• Given some samples, how do you train your network?
• We will write a loop and iteratively update each of the $w$ weights.

Gradient Descent

Notes:

• Think about the $W$ to be the collection of all $w$ weights.
• The key here is still how to compute the derivative, then you plug in $W(t)$ and move in a negative direction.
• $\eta$ is pretty much empirical, and is pretty much this way for all training models, but the hard part is the gradient part.

Gradient of Ein

We need

Notes:

• To compute the gradient, pretty much you need to repeatedly use the chain rule (Computing this derivative is nothing but chain rule)
• Instead of going through all the details we will just review the results intuitively.
• Again, you need to know if we have a loss function Ein, you compute the loss function of every sample and then you do a summation of all of those
  • If you can get the loss for a single sample, then you can just do summation of all the samples to get the total loss
  • We just need to get the gradient of a single sample and then just do a summation.

Algorithmic Approach

$\mathrm{e}(\mathrm{x})$ is a function of ${\mathrm{s}}^{(\ell )}$ and ${\mathrm{s}}^{(\ell )}={\left({\mathrm{W}}^{(\ell )}\right)}^{\mathrm{T}}{\mathrm{x}}^{(\ell -1)}$

sensitivity

Notes:

• We need to derive one more thing, called sensitivity.
  • Above is the definition of sensitivity
  • It is a vector, and there is a sensitivity for each layer
  • It is the partial derivate of the error (just a number) in terms of the partial derivative of each element of $s^{(\ell )}$ (the input vector into this layer)
• But what does sensitivity measure?
  • Look at it element-wise
  • Basically it measures how much the input affects the error (e)
  • This is essentially the idea of a partial derivative, if you have a unit change of the input, how much the output would change?
    • Think of getting the derivative of y = 2x in terms of y?
    • It is just 2, this means if the input is increased by one unit, the output is increased by two units.
  • If we have unit change in the input, how much will it change on e?
  • If the sensitivity for a unit is 0, it will not affect e

Notes:

• $W$ is the connection between two layers
• So now we want to know the partial derivative of the error in terms of $W$
• Remember rows come from the previous layer (i), and columns come from the next layer (j)
• What we want to answer is: If this $W$ is changed by a small amount, how much will $e$ change?
  • If we have unit change in each of the $W$, how much it changes the error?
• What do we need to know to compute this?
  • Suppose you know the sensitivity of every layer
  • What affects the derivative of $W$?
  • If the sensitivity for a unit is large, that means if we have a small change in one entry, the change in error is large, you do not need to consider anything downstream,
    • The sensitivity basically tells you everything after this layer encoded into a single vector
  • What else is important here?
    • IF the output unit if (i) has a zero value, and the derivative measure if we have unit change with the connection $W$, what would happen here?
    • This output value is multiplied with $W$, then what would happen to j? There is no change, the derivative is 0.
• The derivative of $W$ is simply the output value of (i) times the sensitivity value of (j)
• If you connect all of that into a matrix you get to: ${\mathrm{x}}^{(\ell -1)}{\left({\mathit{\delta }}^{(\ell )}\right)}^{\mathrm{T}}$
  • How can we obtain $x$?
    • Again we are talking about a single sample, because if we can do this for a single sample, we can do this for every sample
    • Just use the [[#Forward Propagation Computing $h(x)$]] formula, if you do forward propagation you get the $x$ for each layer.
• Question: $W$s are randomly initialized, what happens if we initialize $W$ to be all zeroes? what will happen?
  • In logistic regression you can do that because you only have one layer, but what would be the consequence here?
  • This is an exam question, if you have a network of layers, is initializing $W$ to be all zeroes a good idea?
  • It is not a good idea because if we do it (a zero matrix) in forward propagation, the values on the output will be all zero vectors, and with $\theta$, if the input is zero, the output will be zero, so the $x$ of the next layer will be all zeros.
• Takeaway: the derivate in terms of W is proportional to the sensitivity.

Computing ${\delta }^{(\ell )}$ Using the Chain Rule

Multiple applications of the chain rule:

Notes:

• To compute the sensitivity we use backward propagation, we start from the last layer, until we reach the first one.
• All we need to do is given a particular delta, how do we compute the delta from the previous layer
• Delta is a derivate, so we need to backward propagate this derivative, so we are propagating derivatives
• Easier case: Given delta (l), how do we calculate delta (l-1)?
  • Basically you need to know the partial derivative to the output
  • If we know the partial derivative of the output for this layer , how do we calculate the partial derivative of the input.
    • Note you are not propagating the actual value, you are propagating the derivative
  • You have to compute the derivative of $\theta$ to get a function, and then you need to plug in to the value you got from forward propagation
• Why this is important?
  • You can see that if you take the derivate of $\theta (s)$ the derivative will be close to 0.
    • If your input value to $\theta$ is very large, your gradient will be close to 0.
• The backward propagation in some units will depend on the forward propagation, that is why we first need to do forward propagation.
• Why is this non-linear function a curve gradient?
  • When we talk about $\theta$ we are talking about element-wise (each unit)
  • You compute the gradient of $\theta$, and the you plug in.
  • If $W$ has a grater gradient in the output, the input will be close to 0.

Notes:

• How do we backward propagate the W matrix
• It requires two operations
  • We need to first forward propagate
  • Then we need forward propagation
• The weight (each line) needs to be multiplied with the sensitivity on each unit, then we'll sum them up together and get the derivative
• You are taking the ith row and taking the inner product with each sensitivity (each column). This is represented as a matrix multiplication
  • This is because this product eventually becomes a column vector
  • Multiply W matrix with the sensitivity vector, but note you are removing the first element.
  • The 1 does not need to be backward propagated because there is no input for the "1" entry.
• Note that during prediction time you just need forward propagation, but in training you will need to do forward propagation first, then you need to do backward propagation
  • The cost of doing forward propagation is twice the cost of doing backward propagation
    • In forward propagation we do matrix multiplication
    • In forward propagation we again multiply this W but elementwise?
  • This is why training a network is much more expensive.

The Backpropagation Algorithm

Algorithm for Gradient Descent on Ein

• This is the whole training process
• The key is the inner for loop, it will compute the gradient
  • You do not need to implement this loop in HW2, you will just use pytorch function to do this.
• Can do batch version or sequential version (SGD).

Digits Data